学习<创新创新再创新>(1)

By 高焕堂  

歡迎閱讀：

1. 创新创新

     科学家钱学森说过：“艺术上的修养不仅加深了我对艺术作品中那些诗情画意和人生哲理的深刻理解，也让我学会了艺术上大跨度的宏观形象思维。这些东西对启迪一个人在科学上的创新是很重要的。科学上的创新光靠严密的逻辑思维不行，创新的思想往往开始于形象思维，从大跨度的联想中得到启迪，然后再用严密的逻辑加以验证。… 是不是真正的创新，就看是不是敢于研究别人没有研究过的科学前沿问题，而不是别人已经说过的东西我们知道，没有说过的东西，我们就不知道。”（摘自http://news.QQ.com）

     其中最关键的是如何走出自己的碉堡，做大跨度的联想，让成功形象栩栩如生呢？然后如何以严密逻辑逐步检验（实证或否证）呢？如何知道大家都还不知道的东西（Know Unknown）呢？除了钱学森之外，还有无数深具创新能力的人物，他们的创新思维是什么呢？例如，我们都很欣赏孔明的空城计和千古文章《隆中对》，可是孔明并没有写出他“如何思考”空城计，也没有写下他如何构思《隆中对》里的三分天下大策略，只留下大策略，却没有留下其策略创新思维。在本章里，我们尝试来揭开其神秘的面纱。

     杰出的创新和设计人员大多数擅长于溯因（Abductive）逻辑推理。溯因推理是由观察现象（结果）到原因的猜测推导过程。运用这种方法对可能原因而作出假定（Hypothesis）。这种推理受到逻辑规则制约的程度较小，具有高度的灵活性，是一种颇具创造性的推理方法。于是，本章就从溯因推理说起。

2. 溯因推理与创造性

     溯因（Abductive）推理是除了演绎推理、归纳推理之外的第三种逻辑推理方法。它是去猜测现象的可能原因，具有高度灵活性，是具创造性的推理方法。溯因逻辑是<假定-否证>的逻辑，透过检验方式，发现走不通的路，就删除之（减法）。例如，我们可以提出下述假定（Hypothesis）：

     ☆ 熟悉溯因思考，就能拥有诸葛亮（孔明）的高度创意（如三分天下和空城计）。     ☆ 熟悉溯因思考，就像麦肯锡公司一样，展现高度的商业价值。

     接下来，就能试图寻找事实来否证上述的假定。现在，先来看看演绎推理（图4-1），其命题叙述一个前提，于是可从这个已知为事实的前提，推导出结论。如果前提为真，则结论必然为真。溯因推理是根据事物的因果关系的知识，从所观察到的已知结果追溯到其原因的一种推理方式。它是由已知的事实（Q：命题）为推理的逻辑起点，进而依据推理者的背景知识、生活常识等寻找导致该事实的原因（P：结论）；然后建立一个假定性的推理形式：若P则Q。    溯因推理的核心是推理者发现可以建立一项假定；这让溯因推理具有一项重要的价值：它是一个颇具创造性的过程。溯因推理的作用是提出假定。这种推理是从某特定的令人惊讶的事实出发，推导出其解释或原因的假定。这种假定必须经过演绎的推导和归纳的检验来证实或证伪（又称否证）。溯因推理的优点，就是提出一个解释性假定的创造性行为。    其中的假定，通常无法直接加以验证；如果用实验或调查加以证实，也只是得知该假定得到一定程度的支持（或然率）。如果被证伪（否证），则假说就完全被推翻了。因此，（架构）设计师最擅用溯因推理的“假定-否证”行为来删除许多设计选项，就是俗称的删除法。

3. <假定-否证>= 删除法

    在刚才的溯因推理范例中，假定性推理（Hypothesis）的内容就是：若P（车子停在斑马线上），则Q（车子会被开罚单）。一般而言，要去正面性实证这项假定，可能大费周章；然而，却能轻易地从反面去“否证”它。再如天花免疫的范例中，其假定性推理的内容就是<若P则Q>。若基于Q是已知的事实，而发现有~P的原因也会产生Q的结果，就可能否定掉这项假定性推理。另外，当这个<若P则Q>是真时，就表示<若~Q则~P>的推理也是真。基于Q是已知的事实，我们可以观察~Q的现象，然后寻觅其中之一是P原因所产生的结果。只要找到其中之一，就足以否证了这项假定性推理。这也就是俗称的“假定-否证”思维方法。

     我们可以观察~Q的现象，然后从中寻觅其中之一是P原因所产生的结果。只要找到其中之一，就足以否证了这项假定性推理。再如，停在斑马线上的车子，发现了其中一辆或多辆车子没被罚，就否定掉该项假定性推理了。为了更通俗易懂起见，刚才的溯因推理范例，可以简化如下：

（假定性）推理H：车子停在斑马线上都会被开罚单。

 否证：停在斑马线上的车子，发现了其中一辆或多辆车子没被罚，这可以更简单地表现出“假定-否证”的思维。

     其过程是：从某特定的令人惊讶的事实出发（如挤牛奶的女工似乎没有得天花的病例），推导出其解释或原因的假定。依循假定，追溯到其可能的原因。观察~Q的现象，然后从中寻觅其中之一是P原因所产生的结果。只要找到其中之一，就足以否证了这项假定性推理。

     溯因推理方法是由美国哲学家皮尔士（Peirce，C.S.）所提出的。关于对假定的否证，皮尔士提出一个有效的迭代（Iteration）方法（图4-11），他说：“将一个假定分解为较小的逻辑组成部分（议题），每次检验其中一个，然后一个一个地加以检验，直到一个或其中一个解释具有不容质疑的根据为止”。

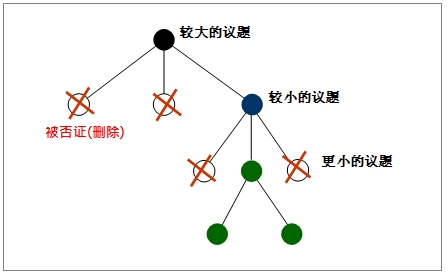
图-1  皮尔士所提出的有效检验方法

     接下来，将以孔明的三分天下大策略来展示这项方法。

** 請繼續閱讀：